Varianza

La varianza es la media de la distancia al cuadrado de los valores de la variable con respecto a la media aritmética.

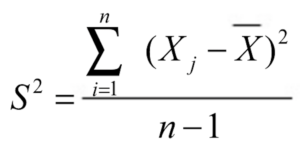
¿Qué es la varianza?

La varianza es una medida estadística de dispersión, que se encarga de determinar la variación de un conjunto de datos con respecto a la media aritmética. De esta forma, entendemos que mide «como de cerca» se encuentran los valores de la media.

Por tanto, representa la suma de residuos (distancia de los valores de la variable a la media) dividida entre el total de observaciones menos uno.

La varianza es una de las tres medidas de dispersión principales, entre las que también se encuentran la desviación típica y el coeficiente de variación. Con la ayuda de estas medidas podemos extraer gran cantidad de información de un conjunto de datos.

¿Cómo se calcula la varianza? Ejemplo

Para aprender a calcularla utilizaremos un ejemplo.

A continuación tenemos un conjunto de datos que vamos a analizar.

En primer lugar debemos calcular la media aritmética. Para ello, dividimos la suma de los valores entre su total.

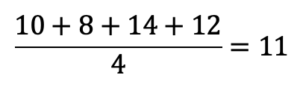
Ahora aplicamos la fórmula a los datos de la variable.

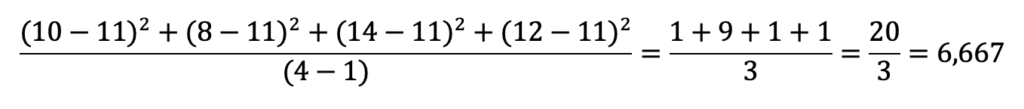
De esta forma sabemos que la varianza de los datos del ejemplo es 6,667.

¿Para qué sirve?

La varianza sirve para saber en qué medida los datos están cerca de la media. De esta forma podemos determinar cómo de robusta es nuestra muestra. Ahora bien, debemos tener en cuenta que esta medida siempre aportará resultados elevados al cuadrado. Aquí es donde entra en juego la desviación típica que es la raíz cuadrada de la varianza, es decir, sin el cuadrado.

Cuanto mayor sea la desviación típica menos robusta será nuestra muestra, mientras que si es reducida indicará que los valores están cerca de la media aritmética, por lo que será más precisa.

¿Tienes alguna pregunta? !No dudes en consultarnos!